vennCycle.gif
vennCycle.gif

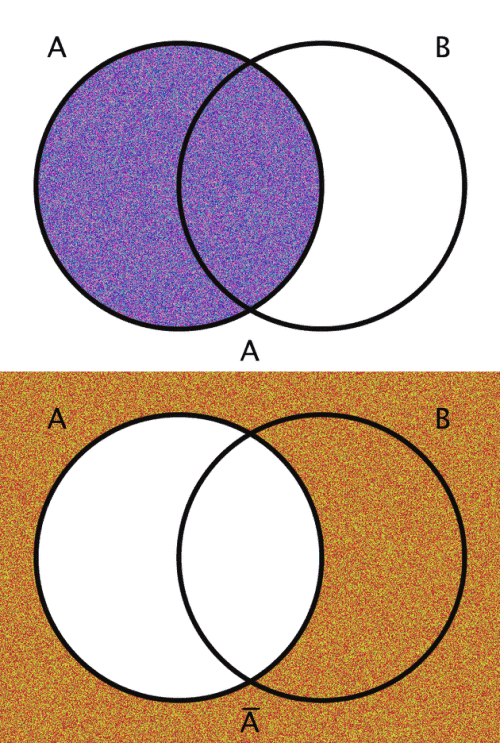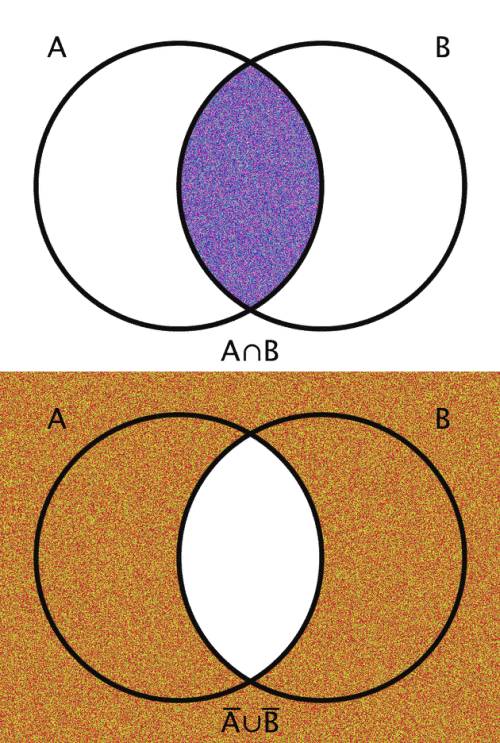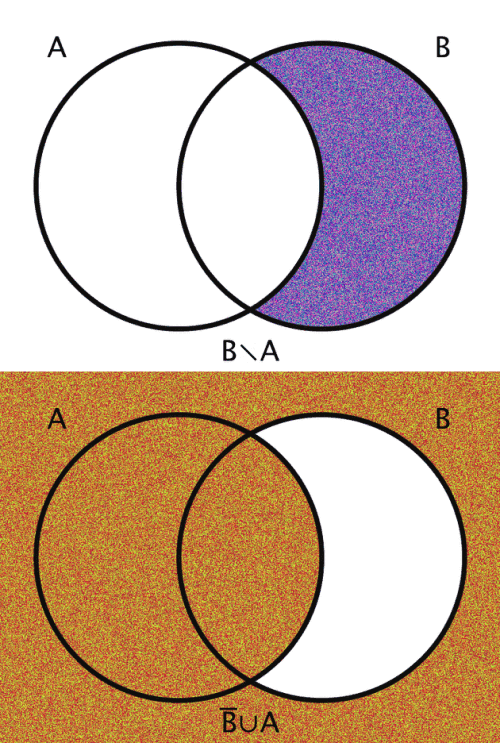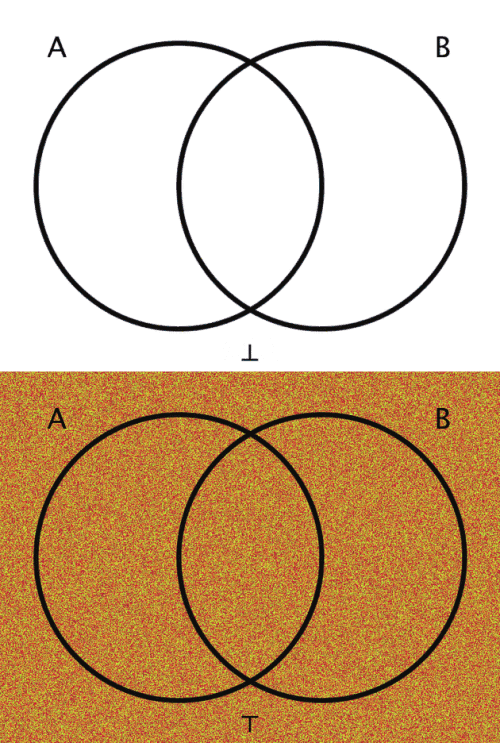
Venn diagrams cane be used to illustrate set-theoretic operations and their negations. Set-theory deals with the ideas of inclusion and exclusion.
|
Symbols and Operators |
Meaning |
Truth Set |
|---|---|---|
| A | The set A | {x | x ∈ A} |
| B | The set B | {x | x ∈ B} |
| A ∩ B | The intersection of A and B | {x | x ∈ A ∧ x ∈ B} |
| A ∪ B | The union of A and B | {x | x ∈ A ∨ x ∈ B} |
| A \ B | The difference of A and B | {x | x ∈ A ∧ x ∉ B} |
| B \ A | The difference of B and A | {x | x ∉ A ∧ x ∈ B} |
| A ∆ B | The symmetric difference of A and B | {x | x ∈ (A \ B) ∨ x ∈ (B \ A)} |
| ⊥ | Contradiction | Trivially false, U̅ |
| A̅ | The complement of set A | {x | x ∉ A} |
| B̅ | The complement of set B | {x | x ∉ B} |
| A̅ ∪ B̅ | The alternative denial of A and B | {x | x ∉ A ∨ x ∉ B } |
| A̅ ∩ B̅ | The joint denial of A and B | {x | x ∉ A ∧ x ∉ B } |
| A̅ ∪ B | The conditional of A and B | {x | x ∉ A ∨ x ∈ B } |
| B̅ ∪ A | The conditional of B and A | {x | x ∈ A ∨ x ∉ B } |
| (A̅ ∩ B̅)∪(A ∩ B) | The biconditional of A and B | {x | x ∈ (A̅ ∩ B̅) ∨ x ∈ (A ∩ B) } |
| ⊤ | Tautology | Trivially true, U |
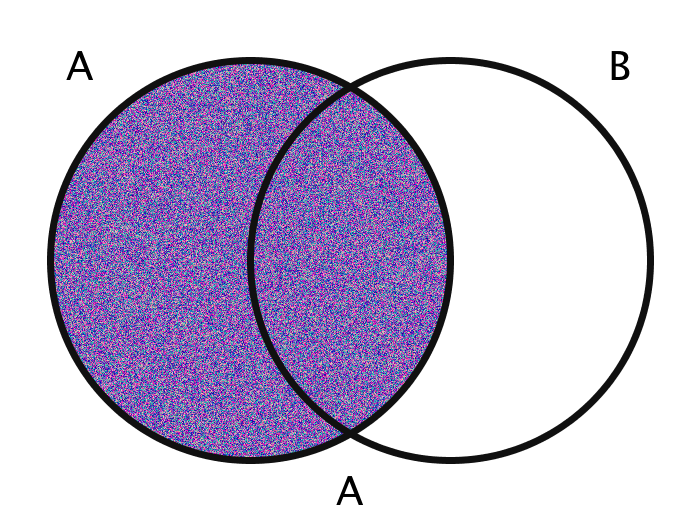
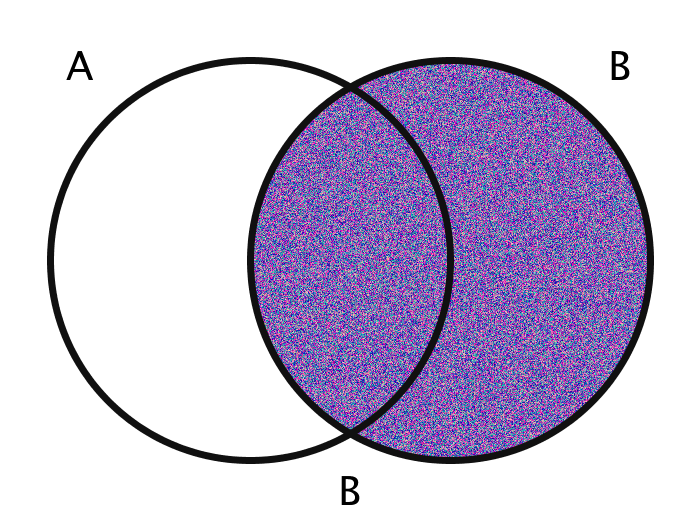
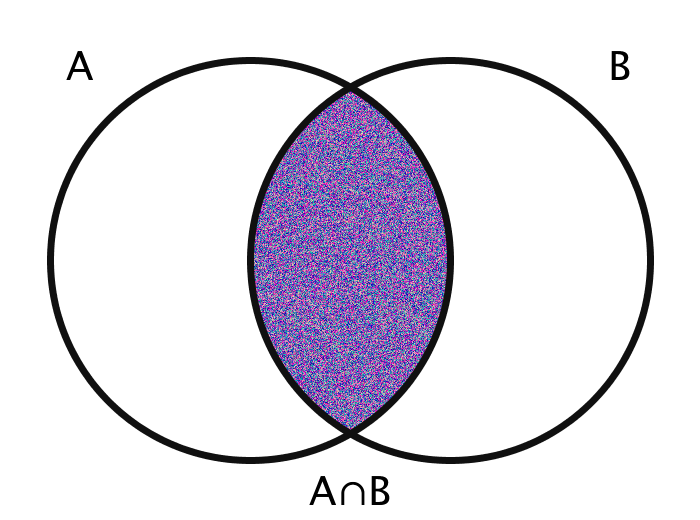
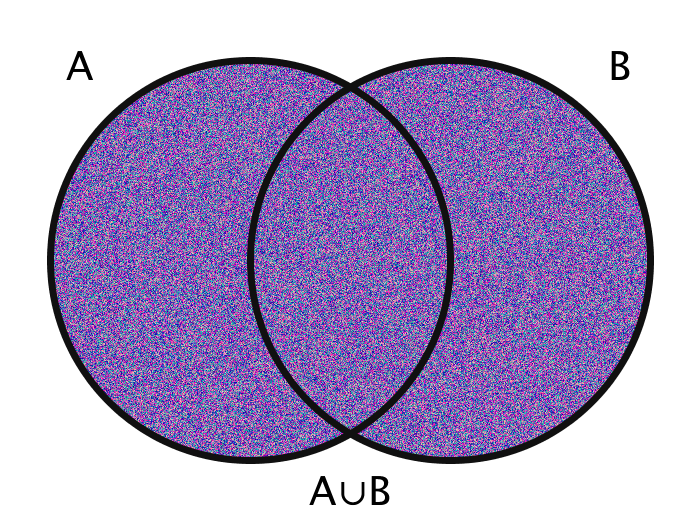
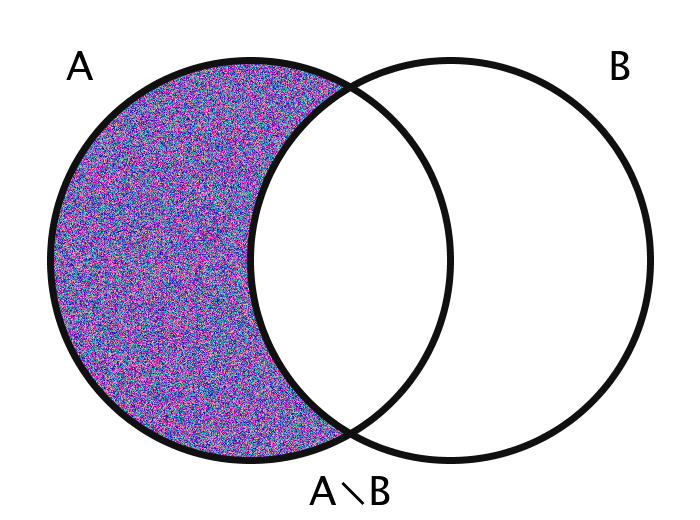
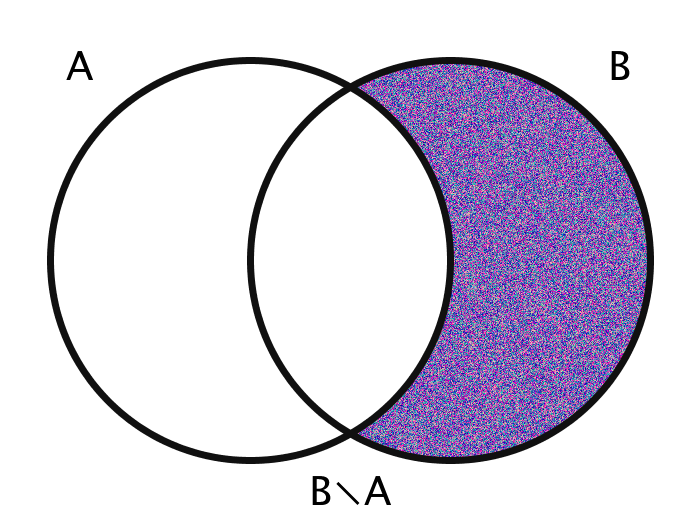
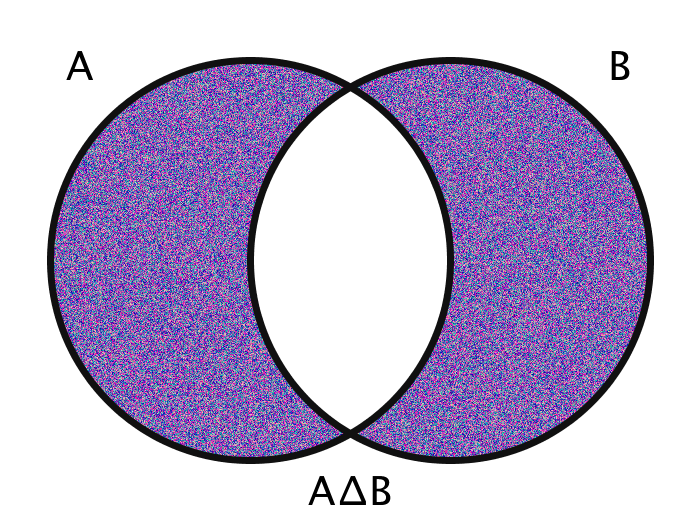
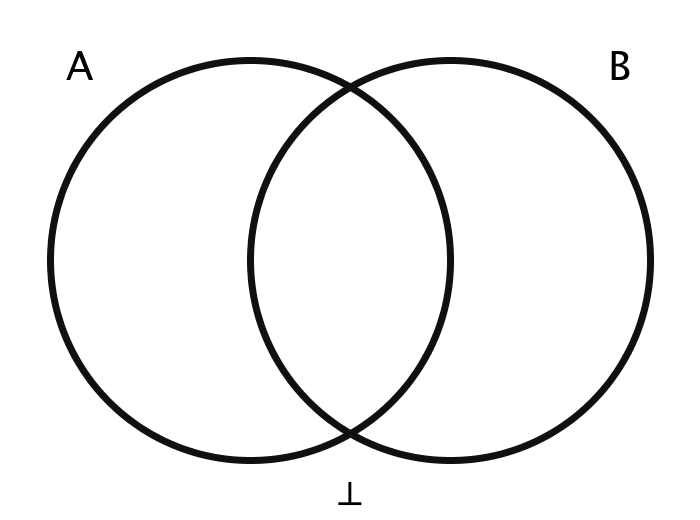
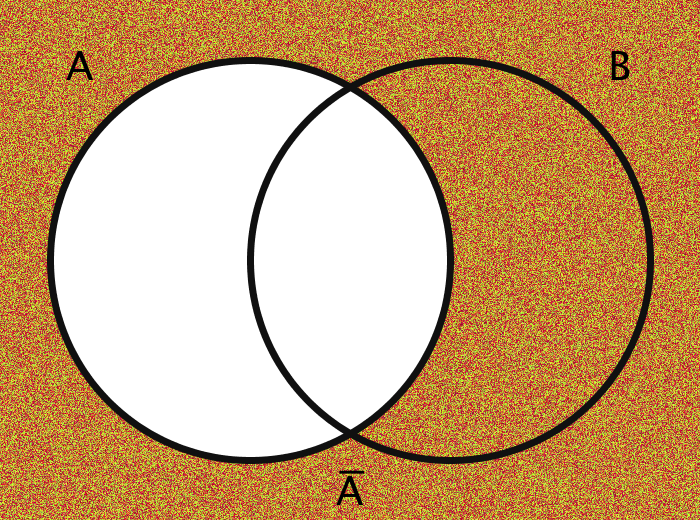
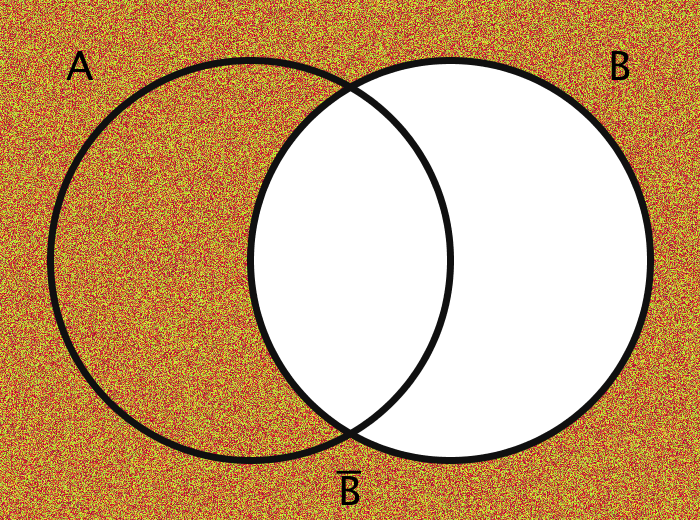
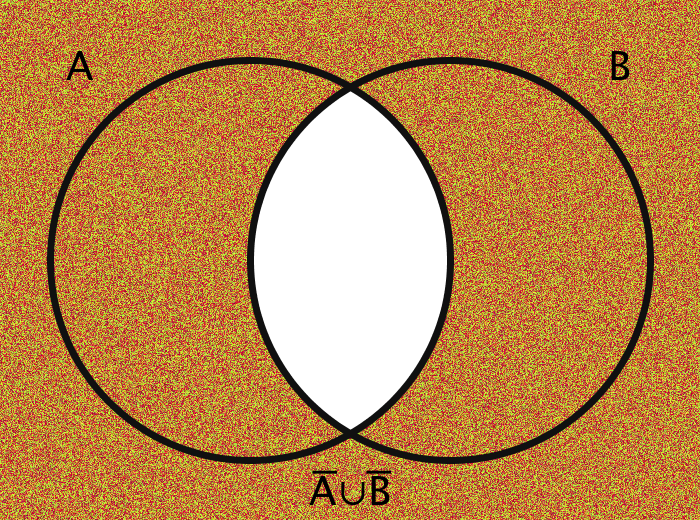
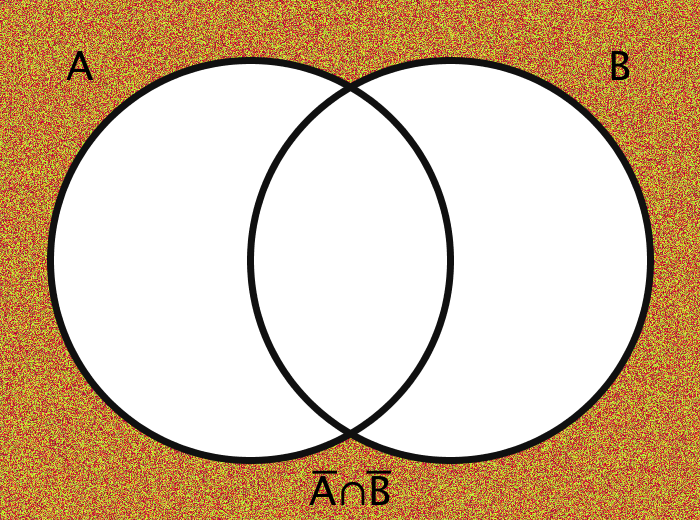
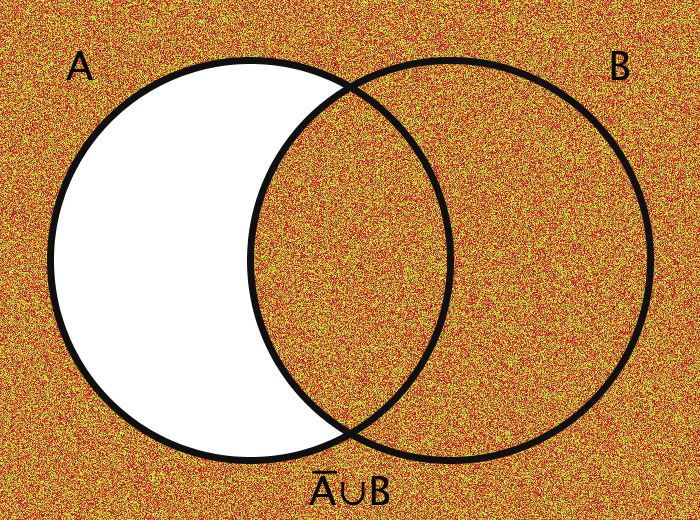
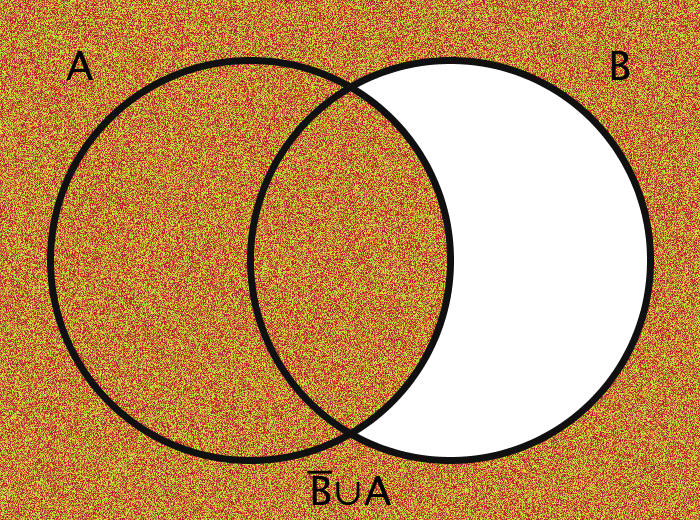
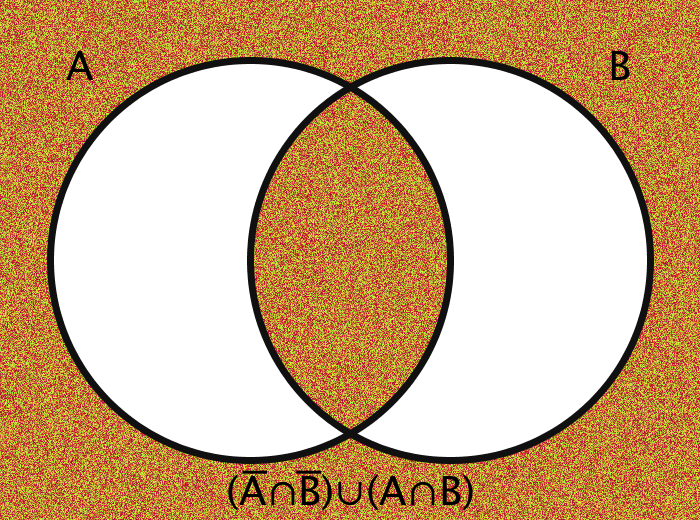
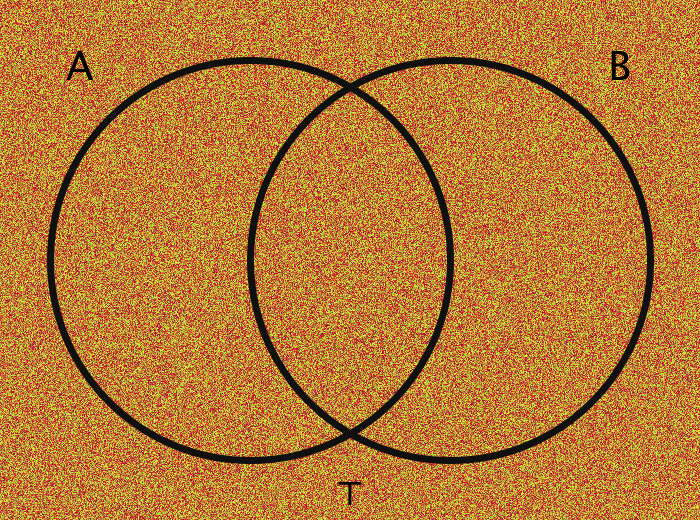
The images are generated using functions encoding these various operations. The actual members of the sets in question are the pixels themselves. Inclusion in the set A, for example, is determined by checking a pixel's geographic location on the screen: does it fall within the circle A?
The area outside the circles (here, for example, the area which is colored orange in every case of the bottom half of the gif) combined with the areas within the circles ought to be thought of in toto as the "Universe" and is commonly labeled as U.
Code: Download vennCircles.zip, vennCirclesNeg.zip || Github
Use the number keys to switch.
Shout-out to John Venn for bringing us the Venn Diagram! What a babe.
